지난 포스팅에서 데이터 정리에 대해 간략하게 알아보았습니다. 이제 완전한 전처리 방법을 배우겠지만 먼저 범주형 데이터 의 통합을 위해 카이제곱 검정알아 보자 이미 들어보셨을 분들을 위해 카이제곱 검정 당신은 아마 그것에 더 익숙합니다.
1. 데이터 통합
기업이나 대규모 데이터베이스에서 데이터 통합은 여러 소스의 데이터를 일관된 저장소로 통합하거나 데이터베이스를 통합하여 이전보다 작은 규모로 모든 데이터를 한 번에 처리하는 방법으로 정의됩니다.
일반적으로 복잡한 계산을 줄이거나 분석을 위한 데이터의 차원을 줄이기 위해 데이터 속성을 통합하는 것을 의미합니다.
앞으로 탐색할 다양한 척도들이 속성 통합의 기준이 된다는 것을 알 수 있습니다.
2. 범주형 데이터: 카이제곱 검정
이제 첫 번째 측정값을 살펴보겠습니다.
첫 번째 방법은 범주형 데이터를 통합하는 데 사용됩니다. 카이제곱 검정 (카이제곱 검정).
$attirubute_i$와 $attribute_j$ 사이에 연관성이 있는지 여부를 카이제곱 검정으로 결정하려면 가설이 필요합니다.
그만큼 귀무 가설호출됩니다
귀무 가설: 두 속성 i와 j는 서로 독립적입니다. 즉, 서로 아무런 관련이 없습니다.
$χ^{2}-테스트$

각 속성 A와 B가 케이스 i와 j를 가질 때 다음과 같이 통계값을 얻는다.
$$e_{ij} = \frac{count(A=a_i)\times{count(B=b_j)}}{n},\;\;\;\;\, χ^{2} = \sum_{ i=1}^c\sum_{j=1}^r\frac{(o_{ij}-e_{ij})^2}{e_{ij}}$$
$e_{ij}$를 계산할 때 귀무 가설이 적용됩니다.
다시 말해서, $e_{ij}$는 두 속성이 서로 독립적이라고 가정하여 얻은 통계값이며,
$o_{ij}$가정 없이 샘플을 조사한 실제 값입니다.
다시 말해서, $o_{ij}$ (실제 관찰) 및 $e_{ij}$ (독립성을 가정한 값)의 차이가 크면 속성 i와 j가 서로 독립적이지 않다는 것을 의미합니다.
따라서 $χ^{2}$가 클수록 두 속성 간의 상관 관계가 커집니다.
$χ^{2}$ 의 인쇄물에서 볼 수 있듯이 두 시그마의 상단이 다릅니다. 즉, 각 속성이 가지는 경우의 수에 관계없이 카이제곱 값을 계산할 수 있음을 의미합니다. 따라서 속성 간의 상관 관계를 식별하는 데 상당히 효율적인 방법이라고 할 수 있습니다.
Essie를 간단히 살펴보고 마무리하겠습니다.
3. 카이제곱 테스트 예
성별 속성 A 및 어떤 정책 약 속성 B와 긍정적/부정적 사례 사이의 상관관계를 찾아봅시다.

각 속성의 값은 위의 표에 나열되어 있습니다. 각각을 기준으로 $e_{ij}$저장하자
$e_{11} = \frac{M\times{Y}}{n} = \frac{450\times{300}}{1500}=90$
$e_{21} = \frac{F\times{Y}}{n} = \frac{1050\times{300}}{1500}=210$
$e_{12} = \frac{M\times{N}}{n} = \frac{450\times{1200}}{1500}=360$
$e_{22} = \frac{F\times{N}}{n} = \frac{1200\times{1050}}{1500}=840$
이제 이 값을 사용하여 카이제곱 값을 찾을 수 있습니다. 모든 $e_{ij}$표로 정리해서 정리해봤습니다.
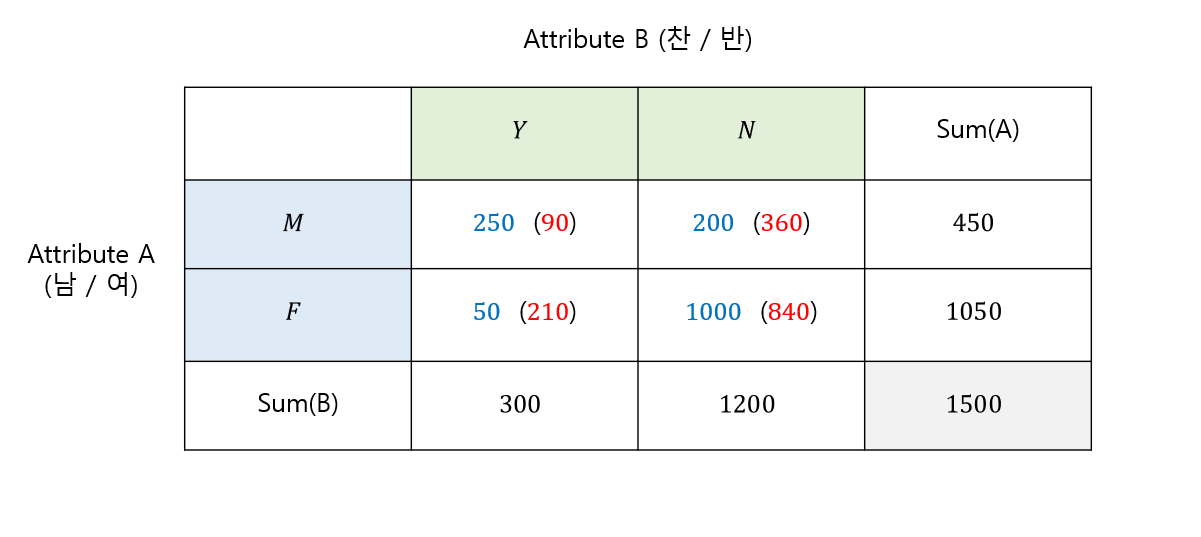
마지막으로 카이제곱 값을 구해봅시다.
$χ^{2} = \frac{(250-90)^2}{90}+\frac{(200-360)^2}{360}+\frac{(50-210)^2}{210 }+\frac{(1000-840)^2}{840}=507.93$
정말 터무니없이 높은 가치입니다.
다시 말해서, 독립 가정(제로 가정) 결코 얻을 수 없는 가치이기 때문에 두 속성은 서로 높은 상관 관계가 있습니다.할수있다.
이런식으로 공식을 배워보고 예제를 통해 카이제곱 검정을 해봤습니다. 계산량은 직접 하기에는 적지 않고, 속성의 경우가 많아질수록 계산량은 늘어나겠지만 우리 주변에는 똑똑한 사람들이 많아서 컴퓨터에서 바로 계산할 수 있는 라이브러리와 함수들이 있다. 정말 멋지고 소중한 분들인 것 같아요(넉죽).
통계학을 공부하신 분들은 아시겠지만 통계학에서의 카이제곱 검정과 같은 의미입니다. 그런데 통계에서는 주로 유의수준과 p값을 이용하여 검정을 하는데 오늘 배운 것은, $χ^{2}$ 직접 값을 가져와서 상관관계를 분석한다는 점에서 조금 다릅니다.
이 게시물에서는 범주형 데이터에 대한 측정값을 살펴보았습니다. 다음 포스트에서는 수치 데이터를 위한 방법을 살펴보겠습니다.
위 글은 한국외국어대학교 의생명공학과 고윤희 교수의 강의(Data Mining for Bioinformatics)를 바탕으로 작성되었습니다.
